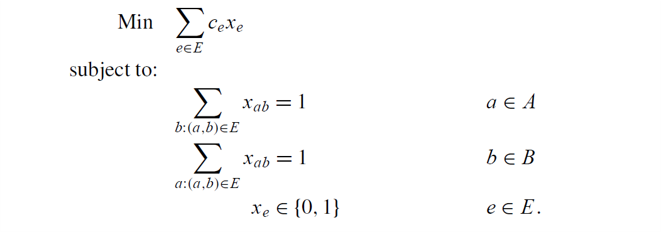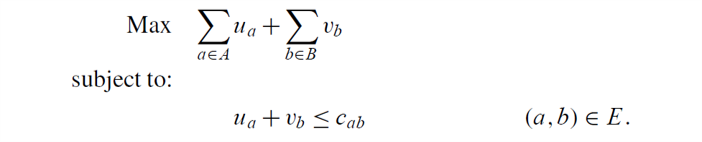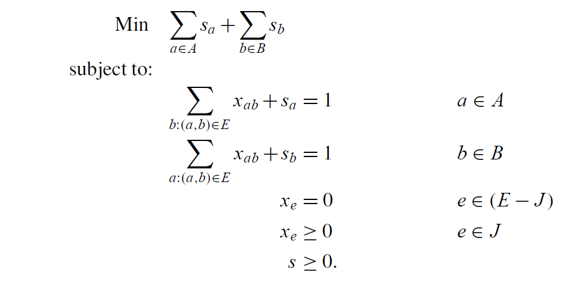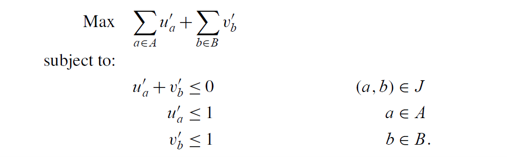Primal Dual Method
看了这本书 The primal-dual
method for approximation algorithms and its application to network
design problems
intro
考虑一个线性规划问题
min c T x s . t . A x ≥ b x ≥ 0
\begin{align*}
\min \quad &c^Tx\\
s.t. \quad Ax&\geq b\\
x&\geq 0
\end{align*}
他的对偶:
max b T y s . t . A T y ≤ c y ≥ 0
\begin{align*}
\max \quad &b^Ty\\
s.t. \quad A^Ty&\leq c\\
y&\geq 0
\end{align*}
根据原问题的 kkt 条件中的互补松弛条件(叫做对偶问题的互补松弛条件):
y T ( A x − b ) = 0
y^T(Ax-b)=0
同样根据对偶问题的 kkt 的互补松弛条件(叫做原问题的互补松弛条件),有
x T ( A T y − c ) = 0
x^T(A^Ty-c)=0
primal dual
方法首先有一个对偶问题的可行解y y x x x x y y y y x x x x I = { i | y i = 0 } , J = { j | A j y = c } I= \{ i|y_i=0 \} ,J= \{j |A^jy=c \} A i A_i A A i i A j A^j A A j j
min ∑ i ∉ I s i + ∑ j ∉ J x j s . t . A x i ≥ b i i ∈ I A x i − s i = b i i ∉ I x ≥ 0 s ≥ 0
\begin{align*}
\min \quad \sum_{i\notin I} s_i&+\sum_{j\notin J} x_j \\
s.t. \quad Ax_i&\geq b_i & i\in I\\
\quad Ax_i-s_i&= b_i & i\notin I\\
x&\geq 0\\
s&\geq 0
\end{align*}
其中s i ( i ∉ I ) s_i(i\notin I) y i ≠ 0 → A i x = b i y_i\not ={0}\rightarrow A_ix=b_i x j ( j ∉ J ) x_j(j\notin J) A j y ≠ c j → x j = 0 A^jy\not ={c_j}\rightarrow x_j=0
如果 restricted primal problem 的最优解是
0,那么说明找到了原问题的一个完全满足互补松弛条件的可行解x x x x y y y y
max b T y ′ s . t . A j y ′ ≤ 0 j ∈ J A j y ′ ≤ 1 j ∉ J y i ′ ≥ − 1 i ∉ I y i ′ ≥ 0 i ∈ I
\begin{align*}
\max \quad &b^Ty'\\
s.t. \quad A^jy'&\leq 0 & j\in J\\
A^jy'&\leq 1 & j\notin J\\
y'_i&\geq -1 & i\notin I\\
y'_i&\geq 0 & i\in I
\end{align*}
这里得说说拉格朗日函数,kkt,线性规划对偶的关系,考虑一个线性规划问题:
min c T x s . t . A x ≥ b x ≥ 0 \begin{align*}
\min \quad &c^Tx\\
s.t. \quad Ax&\geq b\\
x&\geq 0
\end{align*}
把他当成一个约束优化问题,写出拉格朗日函数:
L ( x , λ ) = c T x − λ T ( A x − b )
L(x,\lambda)=c^Tx-\lambda^T(Ax-b)
A x − b ≥ 0 Ax-b\geq 0 c T x ≥ L ( x , λ ) c^Tx\geq L(x,\lambda)
L ( x , λ ) = λ T b − ( c T − λ T A ) x
L(x,\lambda)=\lambda^Tb-(c^T-\lambda^TA)x
如果c T − λ T A > 0 c^T-\lambda^TA> 0 − inf -\inf c T − λ T A ≤ 0 c^T-\lambda^TA\leq 0 λ T b \lambda^Tb
第二种情况就是线性规划的对偶问题了。c T x ≥ L ( x , λ ) ≥ λ T b c^Tx\geq L(x,\lambda) \geq \lambda^Tb
继续考虑 restricted primal problem 的对偶,首先由于 restricted primal
problem 的最优解是大于 0 的,
上面那个对偶问题一定存在一个解y ′ > 0 y'>0 y y y ′ y' y ″ = y + ϵ y ′ y'' =y+\epsilon y' b T y ″ > b T y b^Ty'' >b^Ty ϵ > 0 \epsilon >0
这样可以得到一个更接近最优解的对偶问题可行解。
为了保证 $y’’ $ 是一个对偶问题的可行解,要满足两个条件 1.
y ″ ≥ 0 y'' \geq 0 ϵ ≤ min y i ′ < 0 − y i y i ′ \epsilon \leq \min_{y'_i<0}\frac{-y_i}{y'_i} A T y ″ ≤ c A^Ty'' \leq c ϵ ≤ min A j y ′ > 0 c j − A j y A j y ′ \epsilon \leq \min_{A^jy'>0}\frac{c_j-A^jy}{A^jy'}
得到 $y’’ $
之后重复上面的步骤,每次都能得到一个更接近最优解的对偶问题可行解.
an example
assignment problem (minimum-weight perfect matching problem in bipartite
graphs)
integer program:
example_IP
可以证明 IP 的线性松弛最优解是整数解。
dual of LP relaxation:
example_dual_LP
primal-dual
要从一个对偶问题的可行解开始。取u = v = 0 u=v=0
restricted primal:
rp
I = ∅ , J = { ( a , b ) ∈ E : u a + v b = c a b } I=\emptyset,J=\{(a,b)\in E: u_a+v_b=c_{ab}\}
实际上可以证明 restricted primal 的基本可行解中的变量只能取 0,1.
发现这是在求G = ( A , B , J ) G=(A,B,J)
那么对于任意一个对偶问题的解,我们都能写出 restricted primal 问题,而
restriced primal 问题就是求一个二分图的最大匹配。
如果找到的最大匹配是一个完美匹配,可以发现 restricted primal
的目标函数值为 0,说明找到了最优解,否则,继续写出 restricted primal
的对偶:
dualofrp
二分图上 Maximum matching 的对偶实际上是 vertex cover, 在这里 u 取 -1
表示选择了这个点,取 1 表示没选这个点,max u 恰好是在求最小顶点覆盖
上面对于 assignment problem primal-dual
方法给出了一个精确算法,但是过程中有两个条件难以满足: 1.
问题是由整数规划描述的,线性松弛的最优解恰好是整数解 2. 找到 restricted
primal problem 之后直接发现了图上的对应问题,有已知的算法来解决这个问题
满足不了这两个条件,得到的就是一个近似算法。
整数规划一般不满足强对偶定理,因此对偶问题的最优解一般与原问题最优解不相等;restricted
primal problem 不一定容易解决,那么就放松互补松弛条件 >the central
modification made to the primal-dual method is to enforce the primal
complementary slackness conditions and relax the dual conditions
primal-dual
方法是对偶问题的可行解出发,看是否有能同时满足互补松弛条件和原问题约束的原问题的解,现在由于条件
2 无法满足, restricted primal 及其对偶难解, 我们就只能根据 primal
complementary slackness conditions ,从对偶解来计算原问题的解,而对于
dual
conditions,原问题约束有可能未被满足,有可能取等,有可能不取等,对于对偶问题变量是否取
0 未必有影响,因此只根据未被满足的原问题约束来想办法更新对偶解。
我觉得他的思路大概是这样的。
design rules
(不是记录 design rules,是想搞清楚 design rules 是怎么来的)
原问题一般都能写成这样的整数规划:
min ∑ e ∈ E c e x e s . t . ∑ e ∈ δ ( S ) x e ≥ f ( S ) x e ∈ { 0 , 1 }
\begin{align*}
\min \quad \sum_{e\in E}&c_ex_e\\
s.t. \quad \sum_{e\in \delta(S)}x_e&\geq f(S)\\
x_e&\in \{0,1\}
\end{align*}
δ ( S ) \delta(S) V V S , V − S S,V-S f ( S ) : 2 | V | → 𝐍 f(S):2^{|V|}\rightarrow \mathbf{N}
书中是以 hitting set problem 为例讲解的 design
rules,如果f ( S ) : 2 | V | → { 0 , 1 } f(S):2^{|V|}\rightarrow \{0,1\}
hitting set problem:
Hitting set is an equivalent reformulation of Set
Cover.(放到二分图上,分别是选左边和选右边)
NP-Complete.
Given subsets
T 1 , … , T p T_1,\ldots,T_p E E c e c_e E E A A A ∩ T i ≠ ∅ A\cap T_i\not ={\emptyset} i = 1 , … , p i=1,\ldots,p
hitting set problem 既然是 NP-Complete 问题,很多常见问题都能建立
hitting set 的模型,上面的 IP 是把 ground set 当成图的所有割,需要 hit
的 subsets 当成
f ( S ) = 1 f(S)=1 δ ( S ) \delta(S)
方便起见定义一些符号: *
A = { e : x e = 1 } A=\{e:x_e=1\} y y T 1 , … , T p T_1,\ldots,T_p
根据 part 2 中的 force primal complementary slackness conditions relax
dual CSCs 的方法,
y → 0 y\rightarrow 0 A → ∅ A\rightarrow \emptyset While
∃ k \exists k A ∩ T k = ∅ A\cap T_k=\emptyset
\quad y k y_k ∃ e ∈ T k : ∑ i : e ∈ T i y i = c e \exists e\in T_k : \sum_{i:e\in T_i} y_i=c_e \quad A → A ∪ { e } A\rightarrow A\cup \{e\}
首先在3中,如何选择T k T_k T k T_k
这要根据问题来确定。如果找到了多个T k T_k y k y_k ∃ e ∉ A : ∑ i : e ∈ T i y i = c e \exists e\notin A : \sum_{i:e\in T_i} y_i=c_e
由于整数规划的描述或者 violation oracle
可能没有严格返回f ( S ) = 1 f(S)=1 ≤ \leq ≤ \leq A A A A
fig4.3
c ( A ) = ∑ e ∈ A c e = ∑ e ∈ A ∑ i : e ∈ T i y i = ∑ i = 1 p | A ∩ T i | y i
\begin{align*}
c(A)&=\sum_{e\in A} c_e\\
&=\sum_{e\in A}\sum_{i:e\in T_i}y_i\\
&=\sum_{i=1}^p|A\cap T_i|y_i
\end{align*}
(2th -> 3th line: exchanging the two summations)
令α = max { | A ∩ T i | } \alpha=\max\{|A\cap T_i|\} ∑ y i ≤ O P T \sum y_i\leq OPT
c ( A ) ≤ α O P T
c(A)\leq \alpha OPT
这种计算近似比的方法必须要得到 A
之后才能算出α \alpha B B B B A A B B | A f ∩ T i | ≤ | B ∩ T i | |A_f\cap T_i|\leq |B\cap T_i| A f A_f A A B B | B ∩ T i | |B\cap T_i| β \beta c ( A ) ≤ β O P T c(A)\leq \beta OPT
再考虑 design rules 中的 violated set. 如果考虑每次取出的 violated set
𝒱 j \mathcal{V}_j
y i = ∑ j : T i ∈ 𝒱 j ϵ j y_i=\sum_{j:T_i\in \mathcal{V}_j}\epsilon_j
那么
∑ i = 1 p y i = ∑ i = 1 p ∑ j : T i ∈ 𝒱 j ϵ j = ∑ j = 1 l | 𝒱 j | ϵ j
\begin{align*}
\sum_{i=1}^p y_i&=\sum_{i=1}^p\sum_{j:T_i\in \mathcal{V}_j}\epsilon_j\\
&=\sum_{j=1}^{l} |\mathcal{V}_j|\epsilon_j
\end{align*}
∑ i = 1 p | A f ∩ T i | y i = ∑ i = 1 p | A f ∩ T i | ∑ j : T i ∈ 𝒱 j ϵ j = ∑ j = 1 l ( ∑ T i ∈ 𝒱 j | A f ∩ T i | ) ϵ j
\begin{align*}
\sum_{i=1}^p|A_f\cap T_i|y_i&=\sum_{i=1}^p|A_f\cap T_i|\sum_{j:T_i\in \mathcal{V}_j}\epsilon_j\\
&=\sum_{j=1}^l(\sum_{T_i\in \mathcal{V}_j}|A_f\cap T_i|)\epsilon_j
\end{align*}
比较∑ j = 1 l ( ∑ T i ∈ 𝒱 j | A f ∩ T i | ) ϵ j \sum_{j=1}^l(\sum_{T_i\in \mathcal{V}_j}|A_f\cap T_i|)\epsilon_j ∑ j = 1 l | 𝒱 j | ϵ j \sum_{j=1}^{l} |\mathcal{V}_j|\epsilon_j
if, for all
j ∈ [ l ] j\in[l]
∑ i = 1 p | A f ∩ T i | ≤ γ | 𝒱 j |
\sum_{i=1}^p |A_f\cap T_i|\leq \gamma|\mathcal{V}_j|
then
∑ i = 1 p | A f ∩ T i | y i = ∑ i = 1 p | A f ∩ T i | ∑ j : T i ∈ 𝒱 j ϵ j = ∑ j = 1 l ( ∑ T i ∈ 𝒱 j | A f ∩ T i | ) ϵ j ≤ ∑ j = 1 l γ | 𝒱 j | ϵ j = γ ∑ i = 1 p y i
\begin{align}
\sum_{i=1}^p|A_f\cap T_i|y_i&=\sum_{i=1}^p|A_f\cap T_i|\sum_{j:T_i\in \mathcal{V}_j}\epsilon_j\\
&=\sum_{j=1}^l(\sum_{T_i\in \mathcal{V}_j}|A_f\cap T_i|)\epsilon_j\\
&\leq \sum_{j=1}^l\gamma|\mathcal{V}_j|\epsilon_j\\
&=\gamma\sum_{i=1}^p y_i
\end{align}
这还是需要先计算出A f A_f B B
∑ i = 1 p | A f ∩ T i | ≤ ∑ T i ∈ 𝒱 ( A ) | B ∩ T i | ≤ γ | 𝒱 j |
\sum_{i=1}^p |A_f\cap T_i|\leq \sum_{T_i\in \mathcal{V}(A)}|B\cap T_i| \leq \gamma|\mathcal{V}_j|
同上,γ \gamma
再进一步考虑如果 violation oracle
返回的𝒱 \mathcal{V} f ( S ) = 0 f(S)=0
∑ T i ∈ 𝒱 ( A ) | B ∩ T i | ≤ γ c
\sum_{T_i\in \mathcal{V}(A)}|B\cap T_i| \leq \gamma c
c c 𝒱 ( A ) \mathcal{V}(A) f ( S ) = 1 f(S)=1
design rules 并不是一定最优,只是对于某些问题这样做挺好,对于这些 design
rules 现在都有办法通过分析设计出的近似算法的过程来确定近似比了。
notes
后来在读 the design of approximation algorithms 中的 chap 7.
首先 Theorem 7.1
的定理f = max | { j : e i ∈ S j } | f=\max{|\{j:e_i\in S_j\}|} α \alpha
对于 part2 中说到的近似算法放松互补松弛条件(CSC),这里又更详细的解释:
- enforce primal CSC
意味着如果x i > 0 x_i>0 x i x_i y i > 0 y_i>0
求近似比的部分中f = max | { j : e i ∈ S j } | = ∑ j : e i ∈ S j x j f=\max{|\{j:e_i\in S_j\}|}=\sum_{j:e_i\in S_j}x_j y i > 0 y_i>0
因此 relax dual CSC 保证了近似比,而 enforce primal CSC
提供了通过对偶构造原问题可行解的方法。
整数规划的对偶应该是什么样的?对于同一个问题,不同的整数规划建模的对偶最优解都相同吗?
整数规划没有严格意义上的对偶,但是有个叫拉格朗日对偶的东西。
对于同一个问题不同整数规划建模对偶的最优解是不一样的,不同建模的线性松弛最优解都不一样。
拉格朗日对偶大概是这样的东西:(看了知乎上某人的 integer programming
翻译,我推了一下,但基本上变成 latex 公式输入练习了。。。) part1
中有一点拉格朗日函数和对偶的部分,那里用的原问题是一个线性规划,
把他变成整数规划,加入一个x ∈ X ⊂ Z x\in X\subset Z max λ min x λ T b − ( c T − λ T A ) x \max_{\lambda}\min_{x}\lambda^Tb-(c^T-\lambda^TA)x x ∈ X ⊂ Z x\in X\subset Z λ \lambda
我总觉得这里拉格朗日函数的最小值就是原来的整数规划最优解,但是实际上不是,拉格朗日函数已经是原问题的松弛了,因为在拉格朗日函数中,扔掉了A x − b ≥ 0 Ax-b\geq 0 A x − b ≥ 0 Ax-b\geq 0
IP:
min c T x s . t . A x ≥ b x ≥ 0 x ∈ Z
\begin{align*}
\min \quad &c^Tx\\
s.t. \quad Ax&\geq b\\
x&\geq 0\\
x&\in Z
\end{align*}
构造f ( x ) = c T x − μ T ( A x − b ) ≤ c T x f(x)=c^Tx-\mu^T(Ax-b)\leq c^Tx μ ≤ 0 \mu\leq 0
f ( x ) f(x) g ( μ ) = max μ min x ( c T − μ T A ) x + μ T b g(\mu)=\max_{\mu}\min_{x}(c^T-\mu^TA)x+\mu^Tb
写成线性规划的形式:
min η s . t . ( c T − μ T A ) x 1 + μ T b ≥ η ( c T − μ T A ) x 2 + μ T b ≥ η … ( c T − μ T A ) x n + μ T b ≥ η μ ≥ 0 η ∈ R
\begin{align*}
\min \quad &\eta\\
s.t. \quad
(c^T-\mu^TA)x_1+\mu^Tb&\geq \eta\\
(c^T-\mu^TA)x_2+\mu^Tb&\geq \eta\\
&\ldots\\
(c^T-\mu^TA)x_n+\mu^Tb&\geq \eta\\
\mu &\geq 0\\
\eta &\in R
\end{align*}
然后写出上面的线性规划的对偶:
min ∑ i = 1 n λ i ( c T x i ) s . t . ∑ i = 1 n λ i ( A x i − b ) ≥ 0 ∑ i = 1 n λ i = 1 λ ≥ 0
\begin{align*}
\min \quad \sum_{i=1}^n \lambda_i(c^Tx_i)&\\
s.t. \quad
\sum_{i=1}^n \lambda_i (Ax_i-b)&\geq 0\\
\sum_{i=1}^n \lambda_i &= 1\\
\lambda &\geq 0
\end{align*}
把此处的x i ∈ Z x_i\in Z x i ∈ R x_i\in R x i ∈ R , x i ≥ 0 x_i\in R, x_i\geq 0 x = ∑ i = 1 n λ i x i ∈ R x=\sum_{i=1}^n \lambda_i x_i\in R
这说明了通过调整乘子来让拉格朗日函数的下确界最大的这种这种方法获得的解要比线性松弛的解更好,因为上面有一个把x ∈ Z x\in Z x ∈ R x\in R
然后我就发现了一个问题,观察g ( μ ) = max μ min x ( c T − μ T A ) x + μ T b g(\mu)=\max_{\mu}\min_{x}(c^T-\mu^TA)x+\mu^Tb μ \mu c T − μ T A c^T-\mu^TA x x 0 ≤ x ∈ Z 0\leq x \in Z min \min x x μ \mu ( c T − μ T A ) ≥ 0 (c^T-\mu^TA)\geq 0 x x 𝟎 \mathbf{0} μ T b \mu^Tb
我觉得问题在于:上一段的简单分析应该是没有错误的,这也是为什么 integer
programming 中讲拉格朗日对偶只是把一部分约束放入函数中。在处理的过程中,
A x − b Ax-b x x A x − b ≥ 0 Ax-b\geq 0 x i ∈ Z x_i\in Z x i ∈ R x_i\in R x i x_i x i ∈ R x_i\in R random thoughts
从寒假开始也算是看了两本书关于 primal-dual 方法的章节。
大多数问题的建模都是整数规划,primal-dual
用的是线性松弛的对偶,找到的可行解也不会比线性松弛的最优解更好,
只有线性松弛的解和整数规划相比比较接近才有很好的近似比,如果像是
feedback vertex set 用 hitting set
建模的整数规划,这种线性松弛最优解近似比是 logn 级别, primal-dual
近似比最好也只能做到 logn 级别了,但是最短路的 hitting set
建模线性松弛最优解和整数规划最优解相等,primal-dual
甚至能得出精确算法(dijkstra),
同样的问题,不同的整数规划建模方法,就有不同的线性松弛,就有不同的近似比。
为什么不直接解线性松弛而要用
primal-dual?我觉得主要原因是原来的整数规划约束个数可能是指数级别,解线性规划会解不出,
但是 primal-dual 有时候(Violation Oracle
能很快给出还没满足的约束)需要维护的对偶变量数量只是多项式级别的。
要用 primal-dual 方法解决一个问题,需要考虑 -
用什么方法来写出整数规划,是否能找出一个能用的 Violation
Oracle,线性松弛是否有一个好的近似比 - 根据具体问题是否有好用的 design
rules,按照什么方法和顺序找 violated set 等,复杂度又如何 -
怎么分析近似比,能不能做到线性松弛的近似比一样的级别
我发现大概这个整数规划约束有指数多个,一般整数规划和线性松弛差的不大。
对比 The primal-dual method for approximation algorithms and its
application to network design problems, chapter 4 这个章节和 The Design
of Approximation Algorithms chapter 7,
明显后者更加简单易懂,使用了很多例子,但是我觉得前者要系统很多,而且更加符合逻辑和直觉。首先介绍什么是
classic primal-dual
method,从这个方法出发有了设计近似算法的基本框架,如何从整数规划的线性松弛和
LP 的对偶 找到原问题(IP)的可行解,以及后面对用 hitting set
建模抽象出来的函数f ( S ) f(S)
根据之前看的两本书,做了 slides .